Hydrostatic pressure

we have a tank as shown in figure filled with a liquid of known density. It is filled up to a height  h  from bottom.if we connect a pressure gauge or Pressure transmitter at the bottom of the tank what  pressure will it reads . If the tank is filled with another liquid up to the same height ,what will be the pressure reading?. will it be the same as before? Instead of mounting at the bottom level of the  tank ,if the pressure gauge mounted at some heights above the base of the tank will the pressure gauge reads same pressure ???.
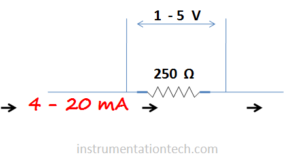
If we use a differential pressure transmitter for liquid level measurement,what should be its range?

 To solve all these questions  we should  understand the concepts of hydrostatic pressure 

 

what is hydrostatic pressure

Hydrostatic pressure is  the pressure excerted by liquid at a point due to its weight above that point . 

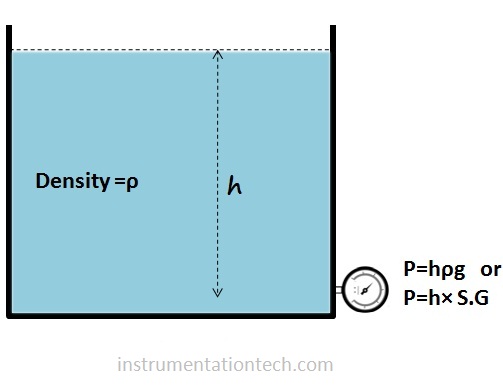
We know about pressure.It is the force acting per unit area

P=F/A

See the tank above .

in the given tank the pressure acting at the bottom surface is  due to the weight of liquid above bottom surface.
As per the definition of pressure which is the force acting per unit area, then pressure acting on the bottom surface equal to
 
  Pressure = Force/Area
 

Here the force is the weight of liquid itself,

W = mass×acceleration due to gravity.

    =  mass × g

       (Mass = volume×Density)

 So pessure   = mass × g / Area
                        = volume  × density  × g/Area
 
Also  (Volume/area = height)
(Also  Volume/area = heigh
 So 
                Pressure  =  height  × density  ×  g      
               
                 P=hρg


if height is expressed in  metres density in kg/m³ and g in m/s² we will get pressure in N/m² or pascal Pa
1N/m² =1Pa
These are the units of pressure in SI system .

We know about pressure.It is the force acting per unit area

P=F/A

See the tank above .

in the given tank the pressure acting at the bottom surface is  due to the weight of liquid above bottom surface.
As per the definition of pressure which is the force acting per unit area, then pressure acting on the bottom surface equal to
 
  Pressure = Force/Area
 

Here the force is the weight of liquid itself, 

                    W = mass×acceleration due to gravity.

                         =  mass × g

        So
 Pressure   = mass × g / Area
massVolume× density = mass
                    = volume  × density  × g/Area           
 Volume× density = mas
                    = height  × density  ×  g                       Volume/area = height
                
                 P=hρg


 if height is expressed in  metres density in kg/m³ and g in m/s² we will get pressure in N/m² or pascal Pa
1N/m² =1Pa
These are the units of pressure in SI system .
So hydrostatic pressure acting at a point depends on height of liquid column above that point and  density or specific gravity of liquid.The value of g is constant ( only negligible differences in values at equators and poles).
  
 So from the equation,   P=hρg , it is clear that
the variation in density and height of the liquid affects the hydrostatic pressure .

Below figure shows a tank filled with a liquid of specific gravity 1.25  .What will be the reading in pressure gauge connected  so that height from pressure gauge to top of the liquid surface is 6m. ? see figure 

 

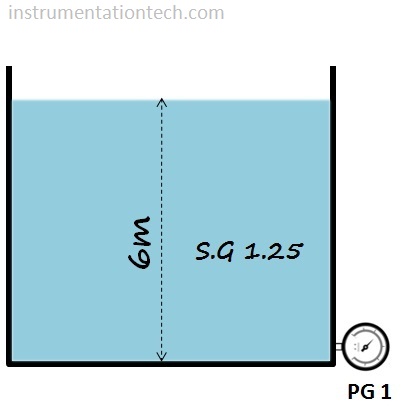
Ans:

      P = hρg

           =6×1250×9.8

           =   73500   Pa

Or P=73.5 KPa

Two tanks as shown in figure filled with different liquids up to same heights .

Which  liquid exerts greater pressure at tank bottom?

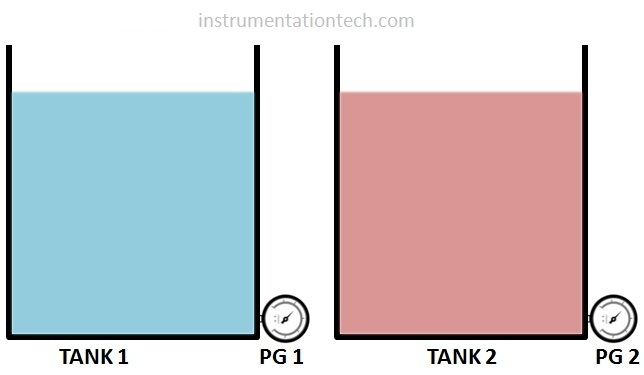
The answer is simple .The tank with heavier liquid  will exerts more pressure. 

As both the tanks are filled up to same heights and their density is different  .So the one with heavier liquid has more density and it exerts more pressure . Remember the equation  P = hρg  ,Here the term h being same for both the tanks .So the one with  heavier ,or greater liquid  density exerts more pressure.

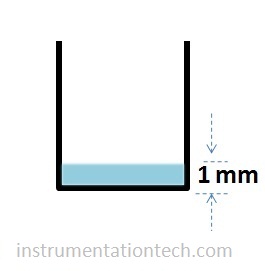
Concept of mmwc unit

See given figure a container  has water to a height of only 1mm!!!!!!!

What is the pressure acting at the bottom of the container.????

We already studied…

          P = hρg

                =0.001×1000×9.8

                =9.8N/m²

                =9.8Pa .

What  if we express this pressure in another unit so that we will get  the pressure in terms of height?

 If we express the pressure due to water with 1 mm of height as 1mmwc ,then it will be better right?

So pressure  acting at the base due to  1mm water height

     =9.8Pa= 1mmwc

          So we have a unit so easy to deal with  in head pressure measurements.we can express pressure due to water head conveniently in units like mmwc , cmwc , inchwc etc

So a 10metre of water inside a tank exerts  a pressure of 10 mwc at the base area of the tank .

or 1000 cmwc

Or 10000mmwc etc……so easy to deal with and  we are getting pressure without decimal point if height is in whole figure.

 

What about other liquids .suppose a tank filled with diesel of specific gravity 0.9( density 900 kg/m³  )up to height of 6metre .what is the pressure acting at the bottom of the tank??

       6000mmwc???

Certainly not. diesel has  density different from water.so obviously head pressure will be different.

How we express this pressure in terms of heights as we have done in water tank.???????

Let’s formulate this.

hydrostatic pressure = height × specific gravity

A tank is filled with a liquid up to certain height say h(l) .Another tank is filled with water of same height.we know water has density 1000 kg/m³.or specific gravity 1. So obviously we know the head pressure will be different  at the bottom because of different specific gravity.

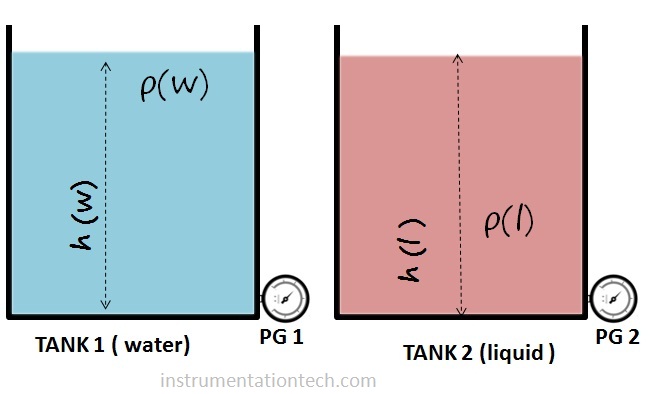
So at what height of  level, in tank1 which is filled with water the  pressure gauge in the water tank will show the same reading of pressure as that in  tank2 which is filled with another  liquid. We need to increase or decrease the level in water tank to attain this .If the unknown  is lighter than water  we need to decrease the level in water tank to acheive equal head pressure at the bottom of the tank and if the liquid is denser we need to increase the level in water tank  to match  the pressure reading of liquid  tank2. 

 So whatever the case, If the pressure on both tank bottoms are equal we can say  

                   h(w)ρ(w)g   = h(l)ρ(l)g

                      h(w)ρ(w)  = h(l )ρ( l)

                                  h(w) = h(l)ρ(l)/ ρ(w)

                                   h(w) = h(l)×S.G

 So height of water column in water tank h(w) needed to attain the same pressure as that of unknown liquid filled up to height h(l) in   liquid tank is given by the above equation.Also we know  orthe height of the water column is simply the pressure and is  expressed in mmwc cmwc etc. pressure in the liquid tank is expressed in terms of height of water column.so the equation can be written as 

                  P=h×S.G (in  mmwc or cmwc ,inches of WC etc)

so back to the question.tank height 6m filled with diesel what is the pressure acting??? 

                So P=h×S.G

                             =6000×0.9

                             =5400 mmwc

So  what is the concept???we expressed the head pressure of diesel with density 900kg/m³ filled up to a height of 6m which is equal to 5400mmwc .In this problem it actually means 6m of diesel will exerts same pressure as that of 5.4m of water(5400mm) which is equal to 5400 mmwc.

(Note:Mercury is also taken as a  reference standard used for head pressure measurements.mmHg,cmHg etc)

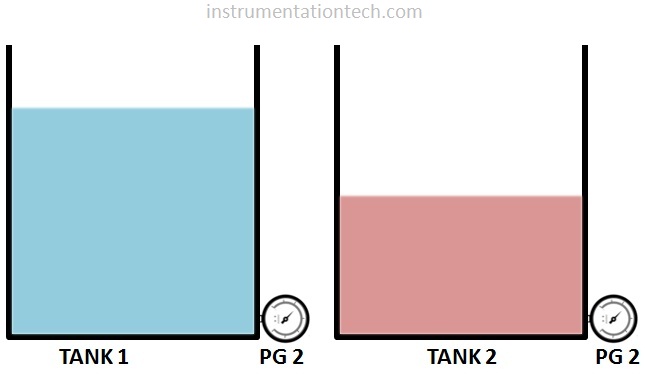
Which pressure gauge reads more? PG1 or pG2? See below figure. 

Ans:We cannot say which one reads more. Data is insufficient to answer . No specific gravity or density is given and also no heights is given.Although level in TANK1  is greater than that in TANK 2 we cannot say the head pressure is greater than that in  TANK 2 . May be the S.G of liquid in TANK2 is high enough so that head pressure  due to that liquid is more than that of Tank 1 liquid..So the data is insufficient for determining which PG reads more.

 

Pressure at the bottom of the tank
 
Q. A tank filled up to a height 6m with a liquid of density 1250kg/m³what is the pressure acting on the bottom of tank?

 

Ans: 

   P = h×S.G

        =6000×1.25

        =7500 mmwc

Does lateral size of tank affects head pressure????

Diameter of  the tank has  no effect on hydrostatic pressure. As we know  p = hfg head pressure is only depend on height and density .

The figure shown  above the pressure acting on PG1 and pressure acting at PG2 are same and is given by,,

                      P   ,= h×S.G

                             =    6000×1.25

                             =   7500 mmwc

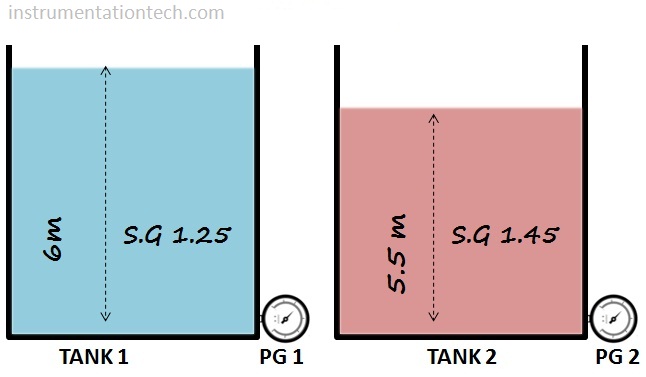
Problem

Two different liquids in two tanks see figure below.Given two pressure gauge connected shows same reading.Then what is the level in tank 2

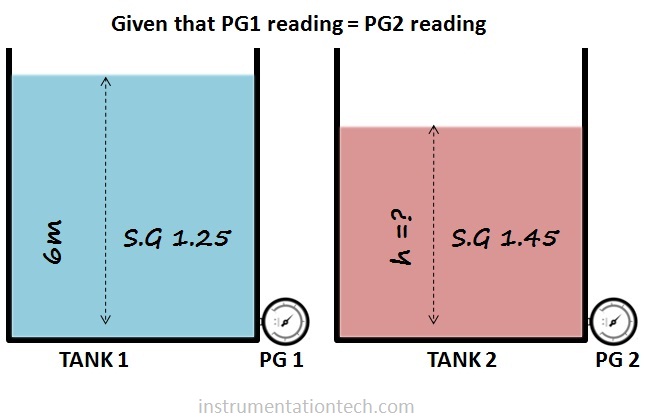
For tank 1

  P 1 = h×S.G

           =6000×1.25

For tank2

P 2   =h×S.G

                                 =h×1.45

 Given P1=P2

         6000×1.25=h×1.45

                             h  = 6000×1.25/1.45

                                   =5172mm

                                    =5.172metres

Try  to solve the problems given below.comment your answer……..

exercise 1

Which pressure gauge reads more? PG1 or pG2? See below figure. 

exercise 2

Which pressure gauge reads more? PG1 or pG2? See below figure. 

exercise 3

Which pressure gauge reads more? PG1 or pG2? See below figure. 

comment your answer.................
Ex1..........

Ex2.............

Ex3..........