Flow and Differential pressure
Differential type flow measurement are employed in many industries like chemical and petrochemical plants, Refineries, water treatment plants etc.Flow measurement using primary elements like orifice plate ,venturi tube ,pitot tube etc are examples of differential pressure type flow measurement .In this method Differential pressure created with the help of these primary elements is measured using a differential pressure transmitters and it is converted to flow as differential pressure varies with flow.This article explains how flow and DP related and differential pressure and flow principles .
Measurement Method
A differential pressure is created in a fluid stream using the primary elements like orifice plate or ventury tube etc.Actually they are flow restrictions which creates high pressure and low pressure points in a flowing fluid in a pipeline. These high pressure and low pressure streams are fed in to a differential pressure transmitter through proper tappings or impulse tubes.These transmitters measures the differencial pressure created .and this DP is related to flow as
Q = k√DP
Where Q is the flow rate
,DP is the differential pressure
and k ,a constant.
DP transmitter either converts this DP in to flow as per this relation and send a signal which is proportional to flow. Or it transmitts a signal which is proportional to DP and this is further converted in to flow in control system side.
Measurement principle
F =K√DP
What is the principle behind the above equation????
How we deduced the equation flow ,F=k√DP in differential pressure method of flow measurements. And why this has square root relationship.
Before deriving this relation you should know about some of the basic concepts related to fluid flow.
Basic Concepts related to fluid flow
1.Equation of continuity for flow
2.Bernaulli’s principle
Equation of continuity's for flow
The figure shows a pipeline with varying diameter through which a incompressible fluid moves . Suppose a a certain amount of fluid enters in to a stream in certain period of time .The same amount of fluid should exit in that period of time otherwise we can say the fluid is compressible and it is compressed .So in our study for the incompressible fluid, we can say the amount of fluid which passes through a cross sectional area in a given time through a pipeline is equal to the amount that passes through another cross sectional area in the same time .
Flow rate at point1 = Flow rate at point2
Q1 =Q2
( Flow = Velocity ×Area Q = V×A)


This is the equation of continuity for flow.It shows flow rate is same through the any section of stream line flow . (For incompressible fluids).A variation in the pipeline diameter causes the the velocity to increase or decrease accordingly and keeps the flow rate same throughout .
Liquids speeds up as they passes from a wider area to a narrow area .You may have noticed a high velocity stream of water jet emerging from a narrow nozzle .Here the velocity of the water actually increases when it is transferred from a high pressurized hose to outside through a narrow nozzle .See below figure .
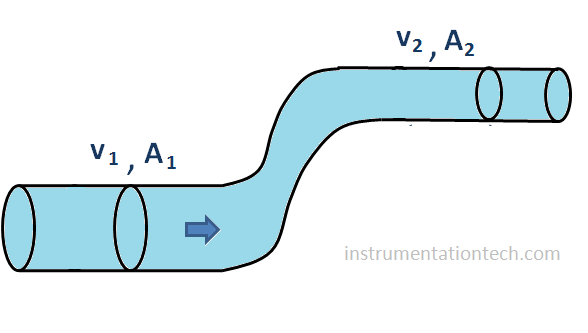

As A2 is smaller than A1 and also the fluid is incompressible,so we can say that an increases in the velociy should happens so that flow rate is same at these two points .So V2 is larger than V1 or velocity increases while the flow area reduces.Or we can say the kinetic energy of the fluid entering into a narrow section from a wider one increases .
Bernaullis Theorem
A great mathematician and scientist,named Daniel bernaulli put forward a theorem to which his name was given .It is the basis of many engineering applications related to fluid motion .
The theorem states that Total energy of flowing fluid is constant
The sum of potential energy,kinetic energy,and pressure energy is constant
That is their sum at one point is equal to the sum at any other point
Kinetic energy+potential energy+pressure energy=Constant
Kinetic energy It is the acquired by the fluid particles due to their movement
Potential energyIt is the energy acquired by the fluid particles due to their position.
ie energy associated due to their height from a reference level.
Pressure energyIt is the energy associated due to the applied external pressure .
Bernaulli’s theorem is a statement to the law of conservation of energy and it is very important and useful in various applications in fluid mechanics .
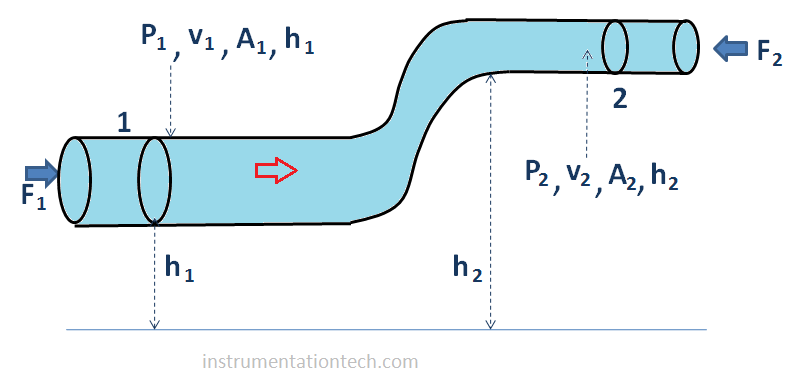
Bernaullis equation
Where
P = static pressure at a given point in a fluid flow .
v = velocity of fluid at a given point
h = height from datum line
ρ= density of fluid .

So from the above equation we can see a change in Pressure head or velocity head or elevation head through the pipeline is compensated .For example for a flow through a horizontal pipeline of varying diameter,a increase in velocity happens at shorter cross section .This means the kinetic energy of the fluid increased at that point . According to low of conservation of energy, some form of energy should drops to make the total energy constant .This can be realized by the pressure drop at the point causing the pressure energy to decrease .
flow and Differential pressure equation
In differential type flow measurement,we already explained flow is formulated from differential pressure .The basic relationship between flow and DP can be deduced from bernaullis equation and equation of continuity of flow .And it looks like,
Flow,
Q=K√DP

Linear and Square root relationship
LINEAR CHARACTERISTICS
Most of the measurement techniques employed in industries to measure various parameters keeps linear behavior between the primary variables and the variables which we need to measure.
For example in level measurement using Dp transmitter , the level and differential pressure keeps linear relationship with each other.
We can say level L= k×Dp
Another example
like magnetic flowmeter , coriolis flow meter,etc keeps linear relationship with its sensed signa
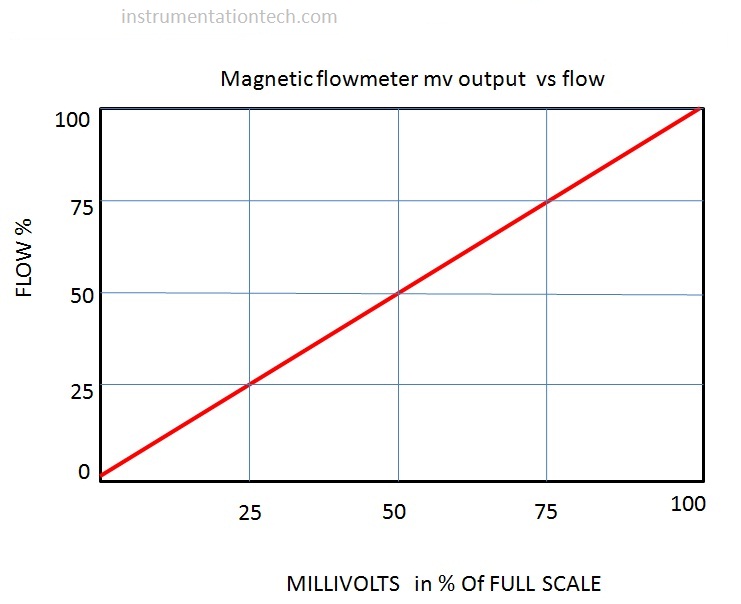
The millivolts reading in magnetic flowmeter keeps linear relationship with flow .If we plot them on x,y axis we will get a straight line. A 25% signal will reads as flow as 25% ,and 50% of full range signal will interpret flow as 50% of full range and so on
SQUARE ROOT CHARACTERISTICS
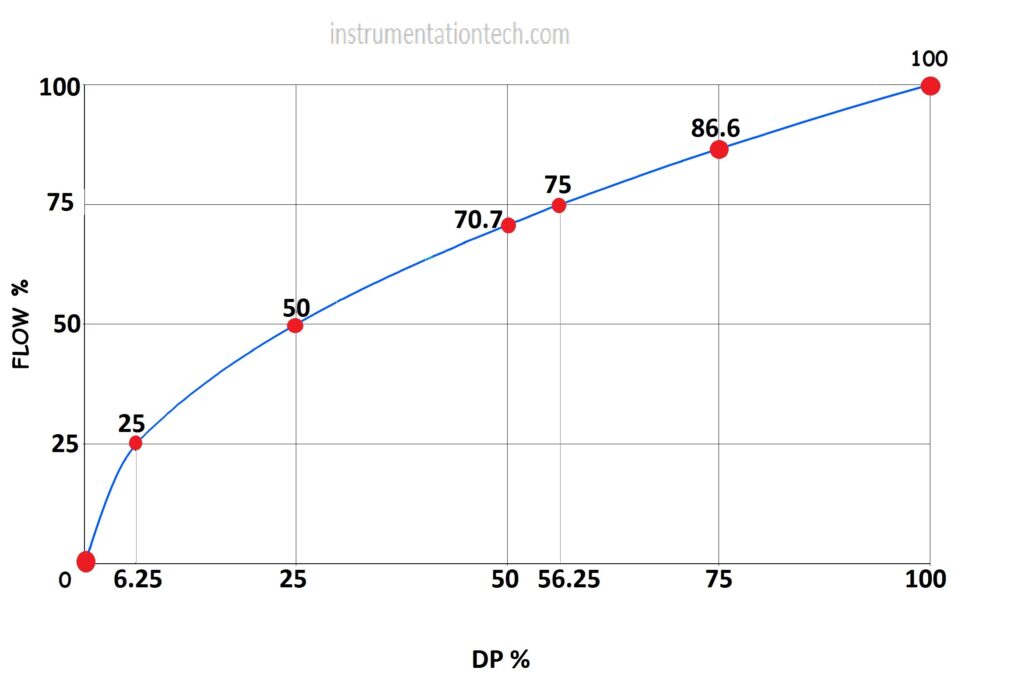
As we already described,Differential pressure type flow instruments like Dp transmitter keeps square root relationship with flow.A 25% of Dp full range is not corresponds to 25% of full range of flow!!!!!!!when Dp is 25% flow is 50% when Dp is 50% flow is 70.9%…etc.If we plot Dp and flow on x and y axis respectively, then we will get a parabolic curve. This is because flow and Dp doesn’t have linear relationship. Flow is relatedly to Dp as
Q = k√Dp
The below figure shows the variation of flow with Differential pressure.Not that the curve is not straight line.It is parabolic
Square root extraction
Square root extraction is the procedure of taking the square root of differential pressure inorder to get flow rate . Because the primary elements creates only a differential pressure .We need to convert it to flow rate.In older times a special device called square root extractor is employed for this procedure.Later with the arrival of modern control systems these square root extractor is replaced by their software counter part. Also modern transmitters were designed for extraction to be done from field side or transmitter itself.